Giải đề thi học kì 1 toán lớp 10 năm 2019 - 2020 sở giáo dục Vĩnh Phúc

 

I. PHẦN TRẮC NGHIỆM (3,0 điểm)

Câu 1. Giải hệ phương trình $\{\begin{array}{c}x+y+z=1\\ 2x-y+z=4\\ x+y+2z=2\end{array}$ ta được nghiệm là:

A. $\left(x;y;z\right)=\left(1;1;1\right)$

B. $\left(x;y;z\right)=\left(2;1;1\right)$

C. $\left(x;y;z\right)=\left(1;-1;1\right)$

D. $\left(x;y;z\right)=\left(1;1;-1\right)$

Câu 2. Chọn khẳng định đúng:

A. $\left\{1\right\}\subset \left[1;\frac{5}{2}\right]$

B. $-2\in \left(-2;6\right)$

C. $1\notin \left[1;\frac{5}{2}\right]$

D. $4\subset \left[3;5\right]$

Câu 3. Trong các câu sau, câu nào là mệnh đề?

A. Chúc các bạn học sinh thi đạt kết quả tốt!

B. Tiết trời mùa thu thật dễ chịu

C. Số $15$ không chia hết cho $2$.

D. Bạn An có đi học không?

Câu 4. Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. $y=-x$                    B. $y=x^2$

C. $y=2x$                      D. $y=x^3$

Câu 5. Cho phương trình $\frac{16}{x^3}+x-4=0$. Giá trị nào sau đây của $x$ là nghiệm của phương trình đã cho?

A. $x=2$                       B. $x=1$

C. $x=3$                        D. $x=5$

Câu 6. Trong mặt phẳng tọa độ $Oxy$, cho $A\left(-1;2\right)$ và $B\left(3;-1\right)$. Tọa độ của vectơ $\overrightarrow{BA}$ là

A. $\left(2;-1\right)$            B. $\left(4;-3\right)$

C. $\left(2;1\right)$               D. $\left(-4;3\right)$

Câu 7. Hàm số $y=\sqrt{1-x}$ có tập xác định là

A. $D=\left(-\infty ;1\right]$

B. $D=\left[1;+\infty \right)$

C. $D=\left(-\infty ;1\right)$

D. $D=\left(1;+\infty \right)$

Câu 8. Parabol $\left(P\right)$ có phương trình $y=a{x}^2+bx+c$ có đỉnh $I\left(1;2\right)$ và đi qua điểm $M\left(2;3\right)$. Khi đó giá trị của $a,b,c$ là

A. $\left(a;b;c\right)=\left(1;-2;-3\right)$

B. $\left(a;b;c\right)=\left(-1;2;-3\right)$

C. $\left(a;b;c\right)=\left(1;2;3\right)$

D. $\left(a;b;c\right)=\left(1;-2;3\right)$

Câu 9. Cho ba điểm $A,B,C$ phân biệt, đẳng thức nào sau đây là sai?

A. $\overrightarrow{BA}-\overrightarrow{CA}=\overrightarrow{BC}$

B. $\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{BC}$

C. $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$

D. $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$

Câu 10. Giải phương trình $\left|x-1\right|=4$ được tập nghiệm

A. $S=\left\{3;5\right\}$

B. $S=\left\{-3;5\right\}$

C. $S=\left\{-3;-5\right\}$

D. $S=\left\{5\right\}$

Câu 11. Cho hai tập hợp $A=\left(-\frac{1}{2};4\right],B=\left[-4;3\right]$. Khi đó $A\cap B$ là

A. $\left(3;4\right)$                  B. $\left[-4;4\right]$

C. $\left[-4;\frac{1}{2}\right)$           D. $\left(-\frac{1}{2};3\right]$

Câu 12. Điều kiện cần và đủ để $\overrightarrow{AB}=\overrightarrow{CD}$ là các vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ thỏa mãn

A. cùng hướng

B. cùng độ dài

C. cùng hướng, cùng độ dài

D. cùng phương, cùng độ dài

II. PHẦN  TỰ LUẬN (7,0 điểm)

Câu 13 (1,0 điểm).  Tìm các tập hợp sau:

$a)\left(-3;2\right)\cap \left[0;5\right]$                                                $b)\left(0;3\right)\setminus \left[2;5\right)$

Câu 14 (1,5 điểm). 

a) Lập bảng biến thiên và vẽ đồ thị của hàm số $y=x^2-2x+2$.

b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=x^2-2x+2$ trên đoạn $\left[-3;2\right]$.

Câu 15 (1,5 điểm).  Giải các phương trình sau:

$a)\left|2x+1\right|=\left|x-2\right|$                                                   $b)\sqrt{2x-5}=x-4$

Câu 16 (1,5 điểm).  Trong mặt phẳng tọa độ $Oxy$, cho tam giác $ABC$ có $A\left(1;4\right),B\left(2;-3\right),C\left(1;-2\right)$ và $D\left(-1;3m+3\right)$.

a) Tìm tọa độ trọng tâm $G$ của tam giác $ABC$.

b) Tìm $m$ để ba điểm $A,B,D$ thẳng hàng.

Câu 17 (0,5 điểm). Cho tam giác $ABC$, gọi $M$ là trung điểm của $BC$, điểm $I$ thỏa mãn $2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}$. Chứng minh $I$ là trung điểm của $AM$.

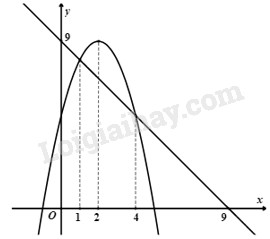
Câu 18 (1,0 điểm). Cho Parabol $\left(P\right)$ có phương trình $y=f\left(x\right)=a{x}^2+bx+c$ và có đồ thị như hình vẽ. Tính giá trị $f\left(-2\right)$.

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

PHẦN I: TRẮC NGHIỆM

1C	2A	3C	4B	5A	6D
7A	8D	9B	10B	11D	12C

 

Câu 1 (NB):

Phương pháp:

Sử dụng máy tính bỏ túi, chứ năng $MODE$ 5, 2.

Cách giải:

Nhập hệ vào máy tính ta được nghiệm $\left(1;-1;1\right)$.

Chọn C.

Câu 2 (TH):

Phương pháp:

Nhận xét tính đúng sai của mỗi đáp án.

Cách giải:

Đáp án A: $\left\{1\right\}\subset \left[1;\frac{5}{2}\right]$ đúng.

Ngoài ra các đáp án B, C, D đều sai.

Chọn A.

Câu 3 (NB):

Phương pháp:

Mệnh đề là một câu khẳng định có tính đúng hoặc sai.

Cách giải:

Đáp án A, B, D không là mệnh đề vì không xét được tính đúng sai cho câu đó.

Đáp án C là mệnh đề đúng.

Chọn C.

Câu 4 (TH):

Phương pháp:

Hàm số $f\left(x\right)$ xác định trên tập đối xứng $D$ là hàm chẵn nếu $f\left(-x\right)=f\left(x\right)$.

Cách giải:

Đáp án A: TXĐ: $D=R$.

Ta thấy $f\left(-x\right)=-\left(-x\right)=x=-f\left(x\right)$ nên hàm số lẻ.

Đáp án B: TXĐ: $D=R$.

Có $f\left(-x\right)={\left(-x\right)}^2=x^2=f\left(x\right)$ nên hàm số chẵn.

Chọn B.

Câu 5 (TH):

Phương pháp:

Thay từng giá trị $x$ đã cho vào phương trình và kiểm tra.

Cách giải:

Với $x=2$ thì $\frac{16}{2^3}+2-4=0$ đúng nên $x=2$ là nghiệm của phương trình.

Chọn A.

Câu 6 (NB):

Phương pháp:

Tọa độ véc tơ $\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)$

Cách giải:

$A\left(-1;2\right)$ và $B\left(3;-1\right)$$\Rightarrow \overrightarrow{BA}=\left(-1-3;2+1\right)=\left(-4;3\right)$.

Chọn D.

Chú ý:

Một số em có thể chọn nhầm B vì tính tọa độ véc tơ $\overrightarrow{AB}$ là sai.

Câu 7 (TH):

Phương pháp:

Biểu thức $\sqrt{f\left(x\right)}$ xác định nếu $f\left(x\right)\ge 0$.

Cách giải:

ĐK: $1-x\ge 0\iff x\le 1$.

TXĐ: $D=\left(-\infty ;1\right]$.

Chọn A.

Câu 8 (VD):

Phương pháp:

Lập hệ phương trình ẩn $a,b,c$ dựa vào các điều kiện bài cho.

Giải hệ tìm $a,b,c$ và kết luận.

Cách giải:

Ta có: $-\frac{b}{2a}=1\iff 2a+b=0$  (1)

Điểm $I\left(1;2\right)\in \left(P\right)\iff 2=a+b+c$  (2)

Điểm $M\left(2;3\right)\in \left(P\right)\iff 3=4a+2b+c$ (3)

Từ (1), (2) và (3) ta có: $\{\begin{array}{c}2a+b=0\\ a+b+c=2\\ 4a+2b+c=3\end{array}\iff \{\begin{array}{c}a=1\\ b=-2\\ c=3\end{array}$

Vậy $\left(a;b;c\right)=\left(1;-2;3\right)$.

Chọn D.

Câu 9 (NB):

Phương pháp:

Nhận xét tính đúng sai của mối đáp án, sử dụng qui tắc ba điểm $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ và $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$.

Cách giải:

Đáp án A: đúng vì $\overrightarrow{BA}-\overrightarrow{CA}=\overrightarrow{BA}+\overrightarrow{AC}=\overrightarrow{BC}$

Đáp án B: sai vì $\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{CA}+\overrightarrow{AB}=\overrightarrow{CB}\ne \overrightarrow{BC}$.

Chọn B.

Câu 10 (TH):

Phương pháp:

Sử dụng kiến thức $\left|A\right|=B>0\iff [\begin{array}{c}A=B\\ A=-B\end{array}$

Cách giải:

$\left|x-1\right|=4$$\iff [\begin{array}{c}x-1=4\\ x-1=-4\end{array}\iff [\begin{array}{c}x=5\\ x=-3\end{array}$

Vậy tập nghiệm của phương trình $S=\left\{-3;5\right\}$.

Chọn B.

Câu 11 (TH):

Phương pháp:

Giao của hai tập hợp là tập hợp chứa các phần tử thuộc cả hai tập hợp.

Cách giải:

Ta có: $A=\left(-\frac{1}{2};4\right],B=\left[-4;3\right]$$\Rightarrow A\cap B=\left(-\frac{1}{2};3\right]$

Chọn D.

Câu 12 (NB):

Phương pháp:

Hai véc tơ bằng nhau nếu chúng cùng hướng và cùng độ dài.

Cách giải:

Điều kiện cần và đủ để $\overrightarrow{AB}=\overrightarrow{CD}$ là chúng cùng hướng và cùng độ dài.

Chọn C.

PHẦN II: TỰ LUẬN

Câu 13 (VD)

Phương pháp

Dùng trục số để tìm giao và hiệu hai tập hợp

Cách giải.

a)  $\left(-3;2\right)\cap \left[0;5\right]=\left[0;2\right)$   

 

$b)\left(0;3\right)\setminus \left[2;5\right)=\left(0;2\right)$                      

 

Câu 14 (VD)

Phương pháp

a) Với $a>0$ thì hàm số $y=a{x}^2+bx+c$ đồng biến trên $\left(-\frac{b}{2a};+\infty \right)$ và nghịch biến trên $\left(-\infty ;-\frac{b}{2a}\right)$

b) Lập BBT của hàm số đã cho trên đoạn $\left[-3;2\right]$ từ đó xác định GTLN và GTNN.

Cách giải.

a) Lập bảng biến thiên và vẽ đồ thị của hàm số $y=x^2-2x+2$.

Tập xác định: $D=R$

Đỉnh Parbol: $I\left(1;1\right)$

BBT:

 

Bảng giá trị:

$x$	-1	0	$1$	2	3
$y$	5	2	$1$	2	5

Đồ thị hàm số:

 

b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=x^2-2x+2$ trên đoạn $\left[-3;2\right]$.

BBT của hàm số $y=x^2-2x+2$ trên đoạn $\left[-3;2\right]$

 

Từ BBT ta có:  GTLN của hàm số trên $\left[-3;2\right]$ là $y=17\iff x=-3$

GTNN của hàm số trên $\left[-3;2\right]$ là $y=1\iff x=1$

Câu 15 (VD)

Phương pháp

a) Giải phương trình dạng $\left|A\left(x\right)\right|=\left|B\left(x\right)\right|\iff [\begin{array}{c}A\left(x\right)=B\left(x\right)\\ A\left(x\right)=-B\left(x\right)\end{array}$

b) Giải phương trình dạng $\sqrt{A\left(x\right)}=B\left(x\right)\iff \{\begin{array}{c}B\left(x\right)\ge 0\\ A\left(x\right)={\left[B\left(x\right)\right]}^2\end{array}$

Cách giải.

$a)\left|2x+1\right|=\left|x-2\right|$

$\iff [\begin{array}{c}2x+1=x-2\\ 2x+1=2-x\end{array}\iff [\begin{array}{c}x=-3\\ x=\frac{1}{3}\end{array}$

Vậy tập nghiệm của phương trình $S=\left\{-3;\frac{1}{3}\right\}$

$b)\sqrt{2x-5}=x-4$ (ĐK: $x\ge \frac{5}{2}$)

$\begin{array}{c}\iff \{\begin{array}{c}x\ge 4\\ 2x-5={\left(x-4\right)}^2\end{array}\\ \iff \{\begin{array}{c}x\ge 4\\ 2x-5=x^2-8x+16\end{array}\\ \iff \{\begin{array}{c}x\ge 4\\ x^2-10x+21=0\end{array}\\ \iff \{\begin{array}{c}x\ge 4\\ [\begin{array}{c}x=3\\ x=7\end{array}\end{array}\Rightarrow x=7\end{array}$

Vậy phương trình có nghiệm $x=7.$

Câu 16 (VD)

Phương pháp

a) Trọng tâm $G$ của tam giác $ABC$ có tọa độ : $\{\begin{array}{c}{x}_G=\frac{x_A+x_B+x_C}{3}\\ y_G=\frac{y_A+y_B+y_C}{3}\end{array}$

b) Ba điểm $A,B,D$ thẳng hàng khi hai véc tơ $\overrightarrow{AB},\overrightarrow{AD}$ cùng phương

Cách giải.

a) Tìm tọa độ trọng tâm $G$ của tam giác $ABC$.

Trọng tâm $G$ của tam giác $ABC$ có tọa độ : $\{\begin{array}{c}{x}_G=\frac{x_A+x_B+x_C}{3}\\ y_G=\frac{y_A+y_B+y_C}{3}\end{array}$

$\iff \{\begin{array}{c}{x}_G=\frac{1+2+1}{3}=\frac{4}{3}\\ y_G=\frac{4+\left(-3\right)+\left(-2\right)}{3}=\frac{-1}{3}\end{array}\Rightarrow G\left(\frac{4}{3};\frac{-1}{3}\right)$

b) Tìm $m$ để ba điểm $A,B,D$ thẳng hàng.

Ta có : $\overrightarrow{AB}=\left(1;-7\right),\overrightarrow{AD}=\left(-2;3m-1\right)$

Ba điểm $A,B,D$ thẳng hàng khi hai véc tơ $\overrightarrow{AB},\overrightarrow{AD}$ cùng phương

Khi đó:$\frac{-2}{1}=\frac{3m-1}{-7}\iff 3m-1=14\iff 3m=15$$\iff m=5$

Vậy $m=5$.

Câu 17 (VD)

Phương pháp

Sử dụng qui tắc trung điểm và qui tắc cộng véc tơ

Cách giải.

Vì $M$ là trung điểm của $BC$ nên $\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}$

Ta có : $2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}$

$\begin{array}{c}\iff 2\overrightarrow{IA}+\overrightarrow{IM}+\overrightarrow{MB}+\overrightarrow{IM}+\overrightarrow{MC}=\overrightarrow{0}\\ \iff 2\left(\overrightarrow{IA}+\overrightarrow{IM}\right)=\overrightarrow{0}\\ \iff \overrightarrow{IA}+\overrightarrow{IM}=\overrightarrow{0}\\ \iff \overrightarrow{IA}=\overrightarrow{MI}\end{array}$

Nên $I$ là trung điểm của $AM.$

Câu 18 (VD)

Phương pháp

Từ hình vẽ ta xác định được trục đối xứng của Parabol và tọa độ một số điểm thuộc đồ thị hàm số

Từ đó xác định hệ số $a,b,c$

Sau đó tính $f\left(-2\right).$

Cách giải.

Gọi đường thẳng cắt parabol trên hình vẽ là $y=mx+n$

Vì đường thẳng cắt trục tung tại $\left(0;9\right)$ và cắt trục hoành tại $\left(9;0\right)$ nên $y=-x+9$

Từ đó tọa độ giao điểm của đường thẳng với Parabol lần lượt là $\left(4;5\right);\left(1;8\right)$

Từ hình vẽ ta thấy parabol có trục đối xứng $x=2$ và đi qua hai điểm có tọa độ $\left(4;5\right);\left(1;8\right)$

Từ đó ta có hệ :

$\begin{array}{c}\{\begin{array}{c}16a+4b+c=5\\ -\frac{b}{2a}=2\\ a+b+c=8\end{array}\iff \{\begin{array}{c}a+b+c=8\\ b+4a=0\\ 16a+4b+c=5\end{array}\\ \iff \{\begin{array}{c}a=-1\\ b=4\\ c=5\end{array}\end{array}$

Nên $\left(P\right):y=f\left(x\right)=-x^2+4x+5$

Suy ra $f\left(-2\right)=-{\left(-2\right)}^2+4\left(-2\right)+5=-7.$