Giải đề thi học kì 1 môn Toán lớp 10 trường THPT Lương Văn Can năm 2020-2021

 

Đề bài

Câu 1(1 điểm). Tìm tập xác định của hàm số $y=\frac{x^2+x+4}{\left(x^2-9\right)\sqrt{x-2}}$

Câu 2(1 điểm). Lập bảng biến thiên và vẽ đồ thị của hàm số $y=x^2-4x+2$

Câu 3( 2 điểm). Cho phương trình $x^2-\left(2m+1\right)x+m^2+2=0$(1)

   a) Tìm m để phương trình (1) có nghiệm $x=2$ và tính nghiệm còn lại

   b) Tìm m để phương trình (1) có 2 nghiệm phân biệt $x_1,x_2$ thỏa: $3x_1{x}_2-5\left(x_1+x_2\right)+6=0$

Câu 4 (3 điểm) Giải các phương trình sau:

   a) $\frac{3x}{x+1}+\frac{x-1}{x}=\frac{2x+1}{x\left(x+1\right)}$

   b) $\left|x^2-1\right|=1-4x$

   c) $\sqrt{x^2-2x+2}=2x-1$

Câu 5(3 điểm). Trong mặt phẳng tọa độ Oxy cho tam giác ABC có $A\left(-1;2\right),B\left(5;4\right),C\left(0;9\right)$.

   a) Chứng minh tam giác ABC cân tại C

   b) Tìm tọa độ của điểm G là trọng tâm tam giác ABC

   c) Tìm tọa độ trực tâm H của tam giác ABC.

Lời giải chi tiết

Câu 1(TH)

Phương pháp:

+) $\frac{f\left(x\right)}{g\left(x\right)}$ xác định nếu $g\left(x\right)\ne 0$.

+) $\frac{1}{\sqrt{f\left(x\right)}}$ xác định nếu $f\left(x\right)>0$.

Lời giải:

Điều kiện xác định của hàm số :

$\{\begin{array}{c}{x}^2-9\ne 0\\ x-2>0\end{array}\iff \{\begin{array}{c}x\ne \pm 3\\ x>2\end{array}\iff \{\begin{array}{c}x\ne 3\\ x>2\end{array}$

Vậy tập xác định của hàm số là :$D=\left(2;+\infty \right)\setminus \left\{3\right\}$

Câu 2(TH)

Phương pháp:

Nếu $a>0$, hàm số đồng biến trên $\left(-\frac{b}{2a};+\infty \right)$ và nghịch biến trên $\left(-\infty ;-\frac{b}{2a}\right)$.

Nếu $a<0$, hàm số đồng biến trên $\left(-\infty ;-\frac{b}{2a}\right)$ và nghịch biến trên $\left(-\frac{b}{2a};+\infty \right)$.

Vẽ đồ thị:

- Có dáng là đường Parabol có đỉnh $\left(-\frac{b}{2a};-\frac{\Delta }{4a}\right),\Delta =b^2-4ac$.

- Trục đối xứng là đường thẳng $x=-\frac{b}{2a}$.

- Bề lõm hướng lên trên khi $a>0$ và hướng xuống dưới khi $a<0$

Lời giải:

Ta có $-\frac{b}{2a}=-\frac{-4}{2.1}=2$.

Hàm số đồng biến trên $\left(2;+\infty \right)$ và nghịch biến trên $\left(-\infty ;2\right)$.

Bảng biến thiên:

 

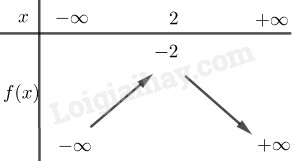
Đồ thị:

Đồ thị nhận đường thẳng $x=2$ làm trục đối xứng. Thay $x=2$ vào hàm số ta được $y=-2$. Đỉnh của đồ thị là $I\left(2;-2\right)$. Đồ thị có bề lõm hướng lên trên.

Đồ thị hàm số cắt trục tung tại $A\left(0;2\right)$ và đi qua các điểm $B\left(1;-1\right),C\left(4;2\right);D\left(-1;7\right)$

Câu 3(VD)

Phương pháp:

a) Thay x=2 vào phương trình tìm m rồi thay m vào phương trình ban đầu tìm nghiệm thứ hai

b) Phương trình $a{x}^2+bx+c=0$ có 2 nghiệm phân biệt khi và chỉ khi $\Delta >0$.

Sử dụng định lý Viét:

$x_1,x_2$ là 2 nghiệm của phương trình $a{x}^2+bx+c=0$. Khi đó:

$\{\begin{array}{c}{x}_1+x_2=-\frac{b}{a}\\ x_1{x}_2=\frac{c}{a}\end{array}$

Lời giải:

a) Thay $x=2$ vào phương trình (1) ta được: $2^2-\left(2m+1\right).2+m^2+2=0$

$\begin{array}{c}\iff m^2-4m+4=0\\ \iff {\left(m-2\right)}^2=0\iff m=2\end{array}$

Thay $m=2$ vào phương trình (1) ta được: $x^2-(2.2+1)x+2^2+2=0$

$\iff x^2-5x+6=0$

$\begin{array}{c}\iff \left(x-2\right)\left(x-3\right)=0\\ \iff [\begin{array}{c}x=2\\ x=3\end{array}\end{array}$

Vậy nghiệm thứ hai của phương trình là $x=3$

b) Phương trình (1) có 2 nghiệm phân biệt khi và chỉ khi $\Delta >0$

$\begin{array}{c}\iff {\left(2m+1\right)}^2-4\left(m^2+2\right)>0\\ \iff 4m-7>0\iff m>\frac{7}{4}\end{array}$

Giả sử (1) có 2 nghiệm phân biệt $x_1,x_2$, theo định lý Viét ta có: $\{\begin{array}{c}{x}_1+x_2=2m+1\\ x_1{x}_2=m^2+2\end{array}$.

Thay vào phương trình  $3x_1{x}_2-5\left(x_1+x_2\right)+6=0$. Ta được:

$\begin{array}{c}3.\left(m^2+2\right)-5\left(2m+1\right)+6=0\\ \iff 3m^2-10m+7=0\\ \iff [\begin{array}{c}m=1\\ m=\frac{7}{3}\end{array}\left(ktm\right)\end{array}$

Vậy không tồn tại giá trị của m thỏa mãn đề bài.

Câu 4(VD)

Phương pháp:

a)

- Bước 1: Đặt điều kiện xác định:

$\frac{f\left(x\right)}{g\left(x\right)}$ xác định nếu $g\left(x\right)\ne 0$.

- Bước 2: Quy đồng mẫu thức, khử mẫu và giải phương trình thu được.

- Bước 3: Kiểm tra điều kiện và kết luận nghiệm.

b) Giải phương trình bằng cách phá dấu giá trị tuyệt đối

$\begin{array}{c}\left|f\left(x\right)\right|=g\left(x\right)\\ \iff [\begin{array}{c}f\left(x\right)=g\left(x\right)khif\left(x\right)\ge 0\\ f\left(x\right)=-g\left(x\right)khif\left(x\right)<0\end{array}\end{array}$

c) Giải phương trình chứa căn thức bậc hai:

$\sqrt{f\left(x\right)}=g\left(x\right)\iff \{\begin{array}{c}g\left(x\right)\ge 0\\ f\left(x\right)=0\end{array}$

Lời giải:

a) $\frac{3x}{x+1}+\frac{x-1}{x}=\frac{2x+1}{x\left(x+1\right)}$(1)

Tập xác định: $D=R\setminus \left\{-1;0\right\}$

$\left(1\right)\iff \frac{3x.x}{\left(x+1\right).x}+\frac{\left(x-1\right).\left(x+1\right)}{x\left(x+1\right)}=\frac{2x+1}{x\left(x+1\right)}$

$\begin{array}{c}\iff \frac{3x^2+\left(x^2-1\right)}{x\left(x+1\right)}=\frac{2x+1}{x\left(x+1\right)}\\ \Rightarrow 4x^2-1=2x+1\\ \iff 4x^2-2x-2=0\\ \iff [\begin{array}{c}x=1\\ x=\frac{-1}{2}\end{array}\left(tm\right)\end{array}$

Vậy tập nghiệm của phương trình là $S=\left\{-\frac{1}{2};1\right\}$