Đề thi học kì 1 môn toán lớp 10 năm 2019 - 2020 trường THPT Kim Liên

 

Mã đề thi 101

I. PHẦN TRẮC NGHIỆM (5,0 điểm – Thời gian làm bài 45 phút).

Câu 1 : Cho phương trình $\left|x-2\right|=2x-1\left(1\right).$ Phương trình nào sau đây là phương trình hệ quả của phương trình $\left(1\right).$

A. ${\left(x-2\right)}^2={\left(2x-1\right)}^2.$

B. ${\left(x-2\right)}^2=2x-1.$

C.$x-2=2x-1.$

D. $x-2=1-2x.$

Câu 2: Cho tập hợp $A.$ Tìm mệnh đề SAI trong các mệnh đề sau ?

A. $A\cap \varnothing =A.$                      B. $\varnothing \subset A.$

C.$A\in \left\{A\right\}.$                         D. $A\subset A.$

Câu 3: Tìm tất cả các giá trị của tham số $m$ để phương trình $\left(m+1\right)x^2-2\left(m+1\right)x+m=0$ vô nghiệm.

A. $m<-1.$                    B. $m\ge -\frac{1}{2}.$

C.$m\le -1.$              D. $-1\le m\le -\frac{1}{2}.$

Câu 4: Cho hình vuông $ABCD$ cạnh bằng $a,$ tâm $O.$ Tính $\left|\overrightarrow{AO}+\overrightarrow{AB}\right|.$

A. $\frac{a\sqrt{10}}{2}.$                                B. $\frac{a\sqrt{3}}{2}.$

C.$\frac{a\sqrt{10}}{4}.$                                 D. $\frac{5a^2}{2}.$

Câu 5: Trong mặt phẳng tọa độ $Oxy$ cho tam giác $ABC$ có $A\left(-4;7\right),B\left(a;b\right),C\left(-1;-3\right).$ Tam giác $ABC$ nhận $G\left(-1;3\right)$ làm trọng tâm. Tính $T=2a+b.$ 

A. $T=9.$                         B. $T=7.$

C.$T=1.$                          D. $T=-1.$

Câu 6: Gọi $S$ là tập các giá trị nguyên của tham số $m$ để hàm số $y=\left(4-m^2\right)x+2$ đồng biến trên $R.$ Tính số phần tử của $S.$

A. $5.$                                       B. $2.$

C. $1.$                                     D. $3.$

Câu 7: Tìm tập xác định của hàm số $y=\sqrt{x-1}+\frac{1}{x+4}.$

A. $\left(1;+\infty \right]\setminus \left\{4\right\}.$

B. $\left(1;+\infty \right)\setminus \left\{4\right\}.$

C.$\left(-4;+\infty \right).$

D. $\left[1;+\infty \right).$

Câu 8: Cho $\overrightarrow{a},\overrightarrow{b}$ có $\left|\overrightarrow{a}\right|=4,\left|\overrightarrow{b}\right|=5,\left(\overrightarrow{a},\overrightarrow{b}\right)={60}^{\circ }.$ Tính $\left|\overrightarrow{a}-5\overrightarrow{b}\right|.$ 

A. $9.$                                 B. $\sqrt{541}.$            C.$\sqrt{59}.$                 D. $\sqrt{641}.$

Câu 9: Trong các phát biểu sau, phát biểu nào là mệnh đề ?

A. $3$ là số nguyên tố lẻ nhỏ nhất.

B. Đề thi hôm nay khó quá!

C.Một tam giác cân thì mỗi góc đều bằng ${60}^{\circ }$ phải không ?

D. Các em hãy cố gắng học tập !

Câu 10: Giả sử $x_1$ và $x_2$ là hai nghiệm của phương trình $:x^2+3x-10=0.$ Tính giá trị $P=\frac{1}{x_1}+\frac{1}{x_2}.$

A. $P=\frac{3}{10}.$                        B. $P=\frac{10}{3}.$

C.$P=-\frac{3}{10}.$                     D. $-\frac{10}{3}.$

Câu 11: Cho hàm số $y=f\left(x\right)=3x^4-4x^2+3.$ Trong các mệnh đề sau, mệnh đề nào đúng ?

A. $y=f\left(x\right)$là hàm số không có tính chẵn lẻ.

B. $y=f\left(x\right)$là hàm số vừa chẵn vừa lẻ.

C. $y=f\left(x\right)$là hàm số chẵn.

D. $y=f\left(x\right)$là hàm số lẻ.

Câu 12: Cho tam giác đều $ABC.$ Tính góc $\left(\overrightarrow{AB},\overrightarrow{BC}\right).$

A. ${120}^{\circ }.$                B. ${60}^{\circ }.$

C.${30}^{\circ }.$                    D. ${150}^{\circ }.$

Câu 13: Điều kiện xác định của phương trình $\sqrt{2x-3}=x-3$ là : 

A. $x\ge 3.$                       B. $x>3.$

C.$x\ge \frac{3}{2}.$                       D. $x>\frac{3}{2}.$

Câu 14: Tìm tất cả các giá trị của tham số $m$ để phương trình $x^2-4x+6+m=0$ có ít nhất $1$ nghiệm dương.

A. $m\le -2.$                  B. $m\ge -2.$

C.$m>-6.$                     D. $m\le -6.$

Câu 15: Hình vẽ dưới là đồ thị của hàm số nào ?

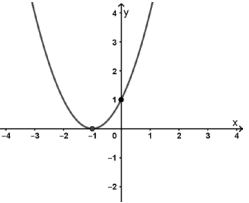
A. $y=-{\left(x+1\right)}^2.$

B. $y=-\left(x-1\right).$

C.$y={\left(x+1\right)}^2.$

D. $y={\left(x-1\right)}^2.$

Câu 16: Số nghiệm phương trình $\left(2-\sqrt{5}\right)x^4+5x^2+7\left(1+\sqrt{2}\right)=0$

A. $0.$                                 B. $2.$

C.$1.$                                  D. $4.$

Câu 17: Tập nghiệm của phương trình $\frac{\left|1-x\right|}{\sqrt{x-2}}=\frac{x-1}{\sqrt{x-2}}$ là :

A. $\left[1;+\infty \right).$                B. $\left[2;+\infty \right).$

C.$\left(2;+\infty \right).$                D. $\left[1;+\infty \right)\setminus \left\{2\right\}.$

Câu 18: Xác định hàm số bậc hai $y=x^2+bx+c,$ biết rằng độ thị hàm số có trục đối xứng là đường thẳng $x=-2$ và đi qua đi $A\left(1;-1\right).$ 

A. $y=x^2+4x-6.$

B. $y=x^2-4x+2.$

C.$y=x^2+2x-4.$

D. $y=x^2-2x+1.$

Câu 19: Tính tổng $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}.$

A. $\overrightarrow{MN}.$                                     B. $\overrightarrow{MP}.$

C.$\overrightarrow{MR}.$                                      D. $\overrightarrow{PR}.$

Câu 20: Mệnh đề nào sau đây là phủ định của mệnh đề “Mọi động vật đều di chuyển” ?

A. Có ít nhất một động vật di chuyển.

B. Có ít nhất một động vật không di chuyển.

C. Mọi động vật đều không di chuyển.

D. Mọi động vật đều đứng yên. 

Câu 21: Cho tam giác $ABC.$ Tìm tập hợp các điểm $M$ thỏa mãn $\left|\overrightarrow{MB}-\overrightarrow{MC}\right|=\left|\overrightarrow{BM}-\overrightarrow{BA}\right|.$

A. Đường tròn tâm $A,$bán kính $BC.$

B. Đường thẳng qua $A$ và song song với $BC.$

C. Đường thẳng $AB.$

D. Trung trực đoạn $BC.$

Câu 22: Tìm tất cả các giá trị của tham số $m$ để phương trình $m^2\left(x+m\right)=x+m$ có tập nghiệm $R?$

A. $m=0$ hoặc $m=1.$

B. $m=0$ hoặc $m=-1.$

C.$m\in \left(-1;1\right)\setminus \left\{0\right\}.$

D. $m=\pm 1.$

Câu 23: Cho $\cos x=\frac{1}{2}.$ Tính biểu thức $P=3{\sin }^{2}x+4{\cos }^{2}x.$

A. $P=\frac{15}{4}.$                B. $P=\frac{13}{4}.$

C. $P=\frac{11}{4}.$                D. $P=\frac{7}{4}.$

Câu 24: Khi nuôi cá thí nghiệm trong hồ, một nhà khoa học đã thấy rằng : Nếu trên mỗi đơn vị diện tích của mặt hồ có $x$ con cá $\left(x\in Z^{+}\right)$ thì trung bình mỗi con cá sau một vụ cân nặng là $480-20x\left(gam\right).$ Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau mỗi vụ thu hoạch được nhiều kg cá nhất ?

A. $10.$                               B. $12.$

C.$9.$                                  D. $24.$

Câu 25: Cho $A=\left(-\infty ;0\right)\cup \left(4;+\infty \right);B=\left[-2;5\right].$ Tính $A\cap B.$ 

A. $\varnothing .$

B. $\left(-\infty ;+\infty \right).$

C.$\left(-2;0\right)\cup \left(4;5\right).$

D. $\left[-2;0\right)\cup \left(4;5\right].$

II. PHẦN TỰ LUẬN (5,0 điểm – Thời gian làm bài 45 phút).

Câu 1: (2 điểm) Cho hàm số $y=-x^2+2x+3.$

a)  (1 điểm) Lập bảng biến thiên và vẽ đồ thị $\left(P\right)$ của hàm số trên.

b) (1 điểm) Tìm điều kiện của tham số $m$ để đường thẳng $y=2mx-4m+3$ cắt $\left(P\right)$ tại $2$ điểm phân biệt có hoành độ lớn hơn $1.$

Câu 2: (1 điểm) Giải phương trình $\left|x-2\right|=x^2-3x-4.$

Câu 3: (2 điểm) Cho hình chữ nhật $ABCD$ có $AD=a,AB=x\left(x>0\right),K$ là trung điểm của $AD.$

a) (1 điểm) Biểu diễn $\overrightarrow{AC},\overrightarrow{BK}$ theo $\overrightarrow{AB},\overrightarrow{AD}.$

b) (0,5 điểm) Tìm $x$ theo $a$ để $AC\perp BK.$

c) (0,5 điểm) Đặt hình chữ nhật $ABCD$ trong hệ trục tọa độ $Oxy$ sao cho $A\left(1;5\right),C\left(6;0\right).$ Gọi $I$ là giao điểm của $BK$ và $AC,$ tìm tọa độ điểm $I.$

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

PHẦN I: TRẮC NGHIỆM

1A	2A	3C	4A	5A
6D	7D	8B	9A	10A
11C	12A	13C	14A	15C
16B	17C	18A	19A	20B
21A	22D	23B	24B	25D

Câu 1 (NB):

Phương pháp:

 Phương trình $\left(2\right)$ được gọi là phương trình hệ quả của phương trình $\left(1\right)$ nếu tập nghiệm của $\left(1\right)$ là tập con của tập nghiệm của $\left(2\right)$.

Phép biến đổi hệ quả cho ta phương trình hệ quả.

Cách giải:

Đáp án A: Phép bình phương là phép biến đổi hệ quả nên ta được phương trình hệ quả.

Chọn A.

Câu 2 (TH):

Phương pháp:

Sử dụng mối quan hệ giữa các tập hợp.

Cách giải:

Đáp án A: Vì $A\cap \varnothing =\varnothing$ nên A sai.

Đáp án B: $\varnothing \subset A$ đúng.

Đáp án C: $A\in \left\{A\right\}$ đúng vì $\left\{A\right\}$ là tập hợp bao gồm các tập hợp.

Đáp án D: $A\subset A$ đúng.

Chọn A.

Câu 3 (TH):

Phương pháp:

Biện luận các trường hợp $a=0,a\ne 0$ và suy ra điều kiện.

Cách giải:

TH1: $m+1=0\iff m=-1$, phương trình trở thành $0x^2-2.0x-1=0\iff -1=0$ (vô nghiệm).

TH2: $m+1\ne 0\iff m\ne -1$, phương trình có ${\Delta }^{\prime }={\left(m+1\right)}^2-m\left(m+1\right)=m+1$.

PT vô nghiệm $\iff {\Delta }^{\prime }<0\iff m+1<0\iff m<-1$.

Vậy để PT vô nghiệm thì $m\le -1$.

Chọn C.

Chú ý:

Một số em có thể quên không xét $m=-1$ và chọn A là sai.

Câu 4 (VD):

Phương pháp:

Tính $\overrightarrow{AO}+\overrightarrow{AB}$ và suy ra độ dài.

Cách giải:

 

Gọi $E$ là trung điểm của $OB$.

Khi đó $\overrightarrow{AO}+\overrightarrow{AB}=2\overrightarrow{AE}$.

$\Delta ABC$ vuông cân tại $B$ có $AB=BC=a$ nên $AC=\sqrt{A{B}^2+B{C}^2}$ $=\sqrt{a^2+a^2}=a\sqrt{2}$

$\Rightarrow AO=OB=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}$ $\Rightarrow OE=\frac{1}{2}OB=\frac{1}{2}.\frac{a\sqrt{2}}{2}=\frac{a\sqrt{2}}{4}$

Tam giác $AOE$ vuông tại $O$ có $AE=\sqrt{A{O}^2+O{E}^2}$ $=\sqrt{\frac{2a^2}{4}+\frac{2a^2}{16}}=\frac{a\sqrt{10}}{4}$

Vậy $\left|\overrightarrow{AO}+\overrightarrow{AB}\right|=2\left|\overrightarrow{AE}\right|=2AE$$=2.\frac{a\sqrt{10}}{4}=\frac{a\sqrt{10}}{2}$

Chọn A.

Câu 5 (TH):

Phương pháp:

Điểm $G$ là trọng tâm tam giác $ABC$ thì $\{\begin{array}{c}{x}_G=\frac{x_A+x_B+x_C}{3}\\ y_G=\frac{y_A+y_B+y_C}{3}\end{array}$

Cách giải:

Điểm $G$ là trọng tâm tam giác $ABC$ thì $\{\begin{array}{c}-1=\frac{-4+a-1}{3}\\ 3=\frac{7+b-3}{3}\end{array}\iff \{\begin{array}{c}-5+a=-3\\ 4+b=9\end{array}$

$\iff \{\begin{array}{c}a=2\\ b=5\end{array}$ $\Rightarrow T=2a+b=2.2+5=9$

Chọn A.

Câu 6 (TH):

Phương pháp:

Hàm số $y=ax+b$ dồng biến trên $R$ nếu $a>0$.

Cách giải:

Hàm số $y=\left(4-m^2\right)x+2$ đồng biến nếu $4-m^2>0\iff m^2<4$ $\iff -2<m<2$

Mà $m\in Z$ nên $m\in \left\{-1;0;1\right\}$, có $3$ giá trị của $m$.

Chọn D.

Câu 7 (NB):

Phương pháp:

Biểu thức $\sqrt{f\left(x\right)}$ xác định nếu $f\left(x\right)\ge 0$.

Biểu thức $\frac{1}{f\left(x\right)}$ xác định nếu $f\left(x\right)\ne 0$.

Cách giải:

ĐK: $\{\begin{array}{c}x-1\ge 0\\ x+4\ne 0\end{array}\iff \{\begin{array}{c}x\ge 1\\ x\ne -4\end{array}\iff x\ge 1$.

Tập xác định $D=\left[1;+\infty \right)$.

Chọn D.

Câu 8 (VD):

Phương pháp:

Tính ${\left|\overrightarrow{a}-5\overrightarrow{b}\right|}^2$, chú ý công thức tính tích vô hướng $\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos \left(\overrightarrow{a},\overrightarrow{b}\right)$.

Cách giải:

Ta có: ${\left|\overrightarrow{a}-5\overrightarrow{b}\right|}^2$$={\left(\overrightarrow{a}-5\overrightarrow{b}\right)}^2={\overrightarrow{a}}^2-10\overrightarrow{a}.\overrightarrow{b}+25{\overrightarrow{b}}^2$$={\left|\overrightarrow{a}\right|}^2-10.\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos \left(\overrightarrow{a},\overrightarrow{b}\right)+25{\left|\overrightarrow{b}\right|}^2$$=4^2-\mathrm{10.4.5.}\cos {60}^0+{25.5}^2=541$

$\Rightarrow \left|\overrightarrow{a}-5\overrightarrow{b}\right|=\sqrt{541}$.

Chọn B.

Câu 9 (NB):

Phương pháp:

Mệnh đề là câu khẳng định xét được tính đúng sai.

Các đáp án B, C, D đều không là mệnh đề.

Cách giải:

Đáp án A: Là mệnh đề đúng.

Chọn A.

Câu 10 (TH):

Phương pháp:

Biến đổi biểu thức làm xuất hiện $x_1+x_2,x_1{x}_2$ và sử dụng Vi-et tính toán.

Cách giải:

Ta có: $ac=1.\left(-10\right)<0$ nên phương trình $x^2+3x-10=0$ luôn có hai nghiệm phân biệt trái dấu $x_1,x_2$ thỏa mãn: $\{\begin{array}{c}{x}_1+x_2=-3\\ x_1{x}_2=-10\end{array}$.

Khi đó $P=\frac{1}{x_1}+\frac{1}{x_2}=\frac{x_1+x_2}{x_1{x}_2}$ $=\frac{-3}{-10}=\frac{3}{10}$

Chọn A.

Câu 11 (TH):

Phương pháp:

Hàm số $f\left(x\right)$ xác định trên tập $D$ đối xứng là hàm số chẵn nếu $f\left(-x\right)=f\left(x\right)$.

Hàm số $f\left(x\right)$ xác định trên tập $D$ đối xứng là hàm số lẻ nếu $f\left(-x\right)=-f\left(x\right)$.

Cách giải:

TXĐ: $D=R$.

Ta có: $f\left(-x\right)=3.{\left(-x\right)}^4-4.{\left(-x\right)}^2+3$ $=3x^4-4x^2+3=f\left(x\right)$

Do đó $f\left(-x\right)=f\left(x\right)$ nên hàm số chẵn.

Chọn C.

Câu 12 (NB):

Phương pháp:

Dựng hình, xác định góc giữa hai véc tơ

Cách giải:

 

Từ hình vẽ ta thấy $\left(\overrightarrow{AB},\overrightarrow{BC}\right)={180}^0-{60}^0={120}^0$.

Chọn A

Câu 13 (NB):

Phương pháp:

Biểu thức $\sqrt{f\left(x\right)}$ xác định nếu $f\left(x\right)\ge 0$.

Cách giải:

ĐK: $2x-3\ge 0\iff x\ge \frac{3}{2}$.

Chọn C.

Chú ý:

Một số em chọn nhầm đáp án A vì nhầm sang điều kiện để bình phương.

Câu 14 (VD):

Phương pháp:

Phương trình có ít nhất một nghiệm dương thì nó có thể có hai nghiệm trái dấu hoặc hai nghiệm đều dương (không nhất thiết phân biệt).

Cách giải:

TH1: Phương trình có hai nghiệm trái dấu $\iff ac<0\iff 1.\left(m+6\right)<0\iff m<-6$.

TH2: Phương trình có hai nghiệm dương (không nhất thiết phân biệt) $\iff \{\begin{array}{c}{\Delta }^{\prime }>0\\ S\ge 0\\ P\ge 0\end{array}\iff \{\begin{array}{c}-m-2\ge 0\\ 2>0\\ m+6\ge 0\end{array}$ $\iff \{\begin{array}{c}m\le -2\\ m\ge -6\end{array}\iff -6\le m\le -2$.

Vậy $[\begin{array}{c}m<-6\\ -6\le m\le -2\end{array}\iff m\le -2$

Chọn A.

Câu 15 (TH):

Phương pháp:

Nhận xét đỉnh, điểm đi qua và đối chiếu các đáp án.

Cách giải:

Quan sát đồ thị ta thấy đồ thị hàm số bậc hai có hệ số $a>0$ nên loại A, B.

Đồ thị hàm số tiếp xúc với trục hoành tại điểm $x=-1$ nên phương trình $y=0$ có nghiệm kép $x=-1$.

Chỉ có đáp án C thỏa mãn.

Chọn C.

Câu 16 (TH):

Phương pháp:

Đặt $t=x^2\ge 0$, nhận xét số nghiệm của phương trình ẩn $t$ và suy ta số nghiệm phương trình ẩn $x$.

Cách giải:

Đặt $t=x^2\ge 0$ ta được $\left(2-\sqrt{5}\right)t^2+5t^2+7\left(1+\sqrt{2}\right)=0$ (1)

PT có $ac=7\left(2-\sqrt{5}\right)\left(1+\sqrt{2}\right)<0$ nên (1) có hai nghiệm $t$ trái dấu.

Do đó phương trình đã cho chỉ có $2$ nghiệm.

Chọn B.

Câu 17 (TH):

Phương pháp:

- Tìm ĐKXĐ.

- Khử mẫu và giải phương trình.

- Kiểm tra điều kiện và kết luận.

Cách giải:

ĐK: $x>2$.

Khi đó PT$\Rightarrow \left|1-x\right|=x-1$ $\iff \left|x-1\right|=x-1$ $\iff x-1\ge 0\iff x\ge 1$.

Kết hợp điều kiện $x>2$ ta được $x>2$.

Vậy tập nghiệm của phương trình là $\left(2;+\infty \right)$.

Chọn C.

Câu 18 (TH):

Phương pháp:

Nhận xét $b,c$ từ điều kiện bài cho và đối chiếu các đáp án.

Cách giải:

Trục đối xứng $x=-2$ nên $-\frac{b}{2.1}=-2\iff b=4$.

Chỉ có đáp án A thỏa mãn.

Chọn A.

Câu 19 (NB):

Phương pháp:

Sử dụng quy tắc ba điểm $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.

Cách giải:

Ta có:

$\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}$

$\begin{array}{c}=\left(\overrightarrow{MN}+\overrightarrow{NP}\right)+\left(\overrightarrow{PQ}+\overrightarrow{QR}\right)\\ +\overrightarrow{RN}\\ =\overrightarrow{MP}+\overrightarrow{PR}+\overrightarrow{RN}\\ =\overrightarrow{MR}+\overrightarrow{RN}\\ =\overrightarrow{MN}\end{array}$

Chọn A.

Câu 20 (NB):

Phương pháp:

Phủ định của mệnh đề $P$ là: “Không phải $P$”

Cách giải:

Phủ định của mệnh đề “Mọi động vật đều di chuyển” là: “Có ít nhất một động vật không di chuyển”

Chọn B.

Câu 21 (VD):

Phương pháp:

Thu gọn các véc tơ ở đẳng thức bài cho và nhận xét.

Cách giải:

Ta có:

$\left|\overrightarrow{MB}-\overrightarrow{MC}\right|=\left|\overrightarrow{BM}-\overrightarrow{BA}\right|$ $\iff \left|\overrightarrow{CB}\right|=\left|\overrightarrow{AM}\right|\iff BC=AM$

Do đó điểm $M$ luôn cách điểm $A$ một khoảng $BC$ cố định.

Vậy $M$ nằm trên đường tròn tâm $A$ bán kính $BC$.

Chọn A.

Câu 22 (TH):

Phương pháp:

Phương trình $ax+b=0$ vô số nghiệm $\iff a=b=0$.

Cách giải:

$m^2\left(x+m\right)=x+m$ $\iff m^{2}x+m^3-x-m=0$ $\iff \left(m^2-1\right)x+m\left(m^2-1\right)=0$

PT có tập nghiệm $R$$\iff \{\begin{array}{c}{m}^2-1=0\\ m\left(m^2-1\right)=0\end{array}$ $\iff \{\begin{array}{c}m=\pm 1\\ m=0,m=\pm 1\end{array}\iff m=\pm 1$

Chọn D.

Câu 23 (TH):

Phương pháp:

Tính ${\sin }^{2}x,{\cos }^{2}x$ và thay vào $P$.

Cách giải:

Ta có: $\cos x=\frac{1}{2}\Rightarrow {\cos }^{2}x=\frac{1}{4}$.

Mà ${\sin }^{2}x+{\cos }^{2}x=1$ $\Rightarrow {\sin }^{2}x=1-{\cos }^{2}x=1-\frac{1}{4}=\frac{3}{4}$.

Vậy $P=3{\sin }^{2}x+4{\cos }^{2}x$ $=3.\frac{3}{4}+4.\frac{1}{4}=\frac{13}{4}$.

Chọn B.

Câu 24 (VD):

Phương pháp:

- Lập hàm số biểu thị số cá thu hoạch được sau mỗi vụ theo $x$.

- Tìm GTLN của hàm số và kết luận.

Cách giải:

Sau mỗi vụ thu hoạch được số gam cá là: $f\left(x\right)=x\left(480-20x\right)=-20x^2+480x$.

Có $-\frac{b}{2a}=-\frac{480}{2.\left(-20\right)}=12$ nên hàm số đạt GTLN tại $x=12$.

Chọn B.

Câu 25 (VD):

Phương pháp:

Tìm giao của hai tập hợp và kết luận.

Cách giải:

Ta có: $A=\left(-\infty ;0\right)\cup \left(4;+\infty \right);$ $B=\left[-2;5\right]$

$\Rightarrow A\cap B=\left[-2;0\right)\cup \left(4;5\right]$.

Chọn D.

PHẦN II: TỰ LUẬN

Câu 1 (VD)

Phương pháp:

a) Tìm trục đối xứng, tọa độ đỉnh, khoảng đồng biến nghịch biến lập bảng biến thiên.

Tìm tọa độ các điểm đi qua và vẽ đồ thị.

b) Xét phương trình hoành độ giao điểm và tìm nghiệm, từ đó suy ra điều kiện.

Cách giải:

a)  (1 điểm) Lập bảng biến thiên và vẽ đồ thị $\left(P\right)$ của hàm số trên.

+) $-\frac{b}{2a}=1;-\frac{\Delta }{4a}=4.$ Đỉnh $I\left(1;4\right).$

+) Trục đối xứng : $x=1.$

+) Bảng biến thiên :

Hàm số đồng biến trên khoảng $\left(-\infty ;1\right)$, nghịch biến trên khoảng $\left(1;+\infty \right).$

Bảng giá trị

$x$	$-1$	$0$	$1$	$2$	$3$
$y$	$0$	$3$	$4$	$3$	$0$

Đồ thị:

Cắt trục $Oy$ tại $\left(0;3\right)$, cắt trục $Ox$ tại $\left(-1;0\right),\left(3;0\right)$.

Có trục đối xứng $x=1$, đỉnh $\left(1;4\right)$.

 

b) (1 điểm) Tìm điều kiện của tham số $m$ để đường thẳng $y=2mx-4m+3$ cắt $\left(P\right)$ tại $2$ điểm phân biệt có hoành độ lớn hơn $1.$

Xét phương trình

$x^2+2\left(m-1\right)x-4m=0\iff [\begin{array}{c}x=2\\ x=-2m\end{array}$

Yêu cầu bài toán $\iff \{\begin{array}{c}-2m>1\\ -2m\ne 2\end{array}\iff \{\begin{array}{c}m<\frac{-1}{2}\\ m\ne -1\end{array}$

$KL:-1\ne m<\frac{-1}{2}.$

Câu 2 (VD): Giải phương trình $\left|x-2\right|=x^2-3x-4.$

Phương pháp:

Phá dấu giá trị tuyệt đối và giải phương trình thu được.

Cách giải:

$\left|x-2\right|=x^2-3x-4.$

+)$x\ge 2,$ ta có phương trình $x^2-4x-2=0\iff [\begin{array}{c}x=2+\sqrt{6}\\ x=2-\sqrt{6}\left(loai\right)\end{array}$

+) $x<2,$ta có phương trình $x^2-2x-6=0\iff [\begin{array}{c}x=1-\sqrt{7}\\ x=1+\sqrt{7}\left(loai\right)\end{array}$

Vậy $S=\left\{2+\sqrt{6};1-\sqrt{7}\right\}$.

Câu 3 (VD)

Phương pháp:

a) Sử dụng quy tắc hình bình hành và xen điểm thích hợp.

b) Hai véc tơ $\overrightarrow{a},\overrightarrow{b}$ vuông góc nếu $\overrightarrow{a}.\overrightarrow{b}=0$.

c) Sử dụng định lí Talet suy ra mối quan hệ giữa các véc tơ $\overrightarrow{AI},\overrightarrow{IC}$.

Cách giải:

a) Biểu diễn $\overrightarrow{AC},\overrightarrow{BK}$ theo $\overrightarrow{AB},\overrightarrow{AD}.$

$ABCD$ là hình chữ nhật nên $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$.

$\overrightarrow{BK}=\overrightarrow{AK}-\overrightarrow{AB}=\frac{1}{2}\overrightarrow{AD}-\overrightarrow{AB}$.

b) Tìm $x$ theo $a$ để $AC\perp BK.$

$AC\perp BK\iff \overrightarrow{AC}.\overrightarrow{BK}=0$$\iff \left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\frac{1}{2}\overrightarrow{AD}-\overrightarrow{AB}\right)=0$

$\iff \frac{1}{2}\overrightarrow{AB}.\overrightarrow{AD}+\frac{1}{2}A{D}^2-A{B}^2-\overrightarrow{AD}.\overrightarrow{AB}=0$

$\iff \frac{1}{2}A{D}^2-A{B}^2=0$ $\iff \frac{1}{2}{a}^2-x^2=0\iff x=\frac{a\sqrt{2}}{2}$.

c) Đặt hình chữ nhật $ABCD$ trong hệ trục tọa độ $Oxy$ sao cho $A\left(1;5\right),C\left(6;0\right).$ Gọi $I$ là giao điểm của $BK$ và $AC,$ tìm tọa độ điểm $I.$

Ta có: $AK//BC\Rightarrow \frac{AI}{IC}=\frac{AK}{BC}=\frac{1}{2}$$\Rightarrow \overrightarrow{AI}=\frac{1}{2}\overrightarrow{IC}$

$\iff \left(x-1;y-5\right)=\frac{1}{2}\left(6-x;-y\right)$

$\iff \{\begin{array}{c}x=\frac{8}{3}\\ x=\frac{10}{3}\end{array}\Rightarrow I\left(\frac{8}{3};\frac{10}{3}\right)$.