Đề kiểm tra 45 phút (1 tiết) - Chương 2, 3 - Đề số 4 - Đại số 10

 

Đề bài

Câu 1.

   a. Vẽ đồ thị hàm số $y=-x^2+4x-3$ .

   b. Xác định các giá trị của m để phương trình $x^2-4\left|x\right|+m=0$ có ít nhất ba nghiệm.

Câu 2.

   a. Giải phương trình $x^2+{\left(\frac{x}{x+1}\right)}^2=3$

   b. Tìm m để phương trình $\frac{x+m-1}{x+1}+\frac{x-2}{x}=2$ vô nghiệm.

Câu 3.Hai nghiệm x₁, x₂ của một phương trình bậc hai thoả mãn các hệ thức $x_1+x_2+x_1{x}_2=0$ và $\left(m-1\right)\left(x_1+x_2\right)-x_1{x}_2=3m-1$

Lập phương trình bậc hai đó.

Câu 4. Xác định m để phương trình $2x+\sqrt{x-1}=m-1$ có nghiệm.

Lời giải chi tiết

Câu 1.

a. Hàm số $y=-x^2+4x-3$ có đồ thị là một parabol với

+ Đỉnh $I(2;1)$

+ Trục đối xứng $x=2$

+ Cắt Oy tại $\left(0;3\right)$ , cắt Ox tại $\left(0;1\right)$  và $\left(0;1\right)$.

Đồ thị

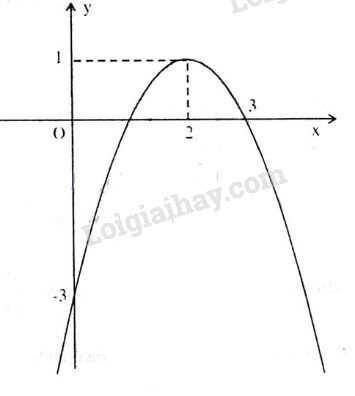
b. Ta có $x^2-4\left|x\right|+m=0$

$\iff -x^2+4\left|x\right|-3=m-3$ .

Phương trình trên là phương trình hoành độ giao điểm của đồ thị hàm số $y=-x^2+4\left|x\right|-3$ và đường thẳng $y=m-3$ .

Hàm số $y=-x^2+4\left|x\right|-3$ là hàm số chẵn nên đồ thị đối xứng qua trục tung.

Khi $x\ge 0$ thì hàm số trở thành $y=-x^2+4x-3$ .

Do đó đồ thị hàm số của hàm số $y=-x^2+4\left|x\right|-3$ bao gồm phần đồ thị hàm số $y=-x^2+4x-3$ ở bên phải trục tung và phần đối xứng của nó qua trục tung.

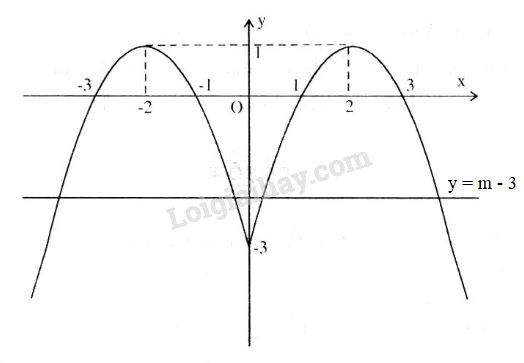
Theo đồ thị phương trình có ít nhất ba nghiệm khi và chỉ khi

$-3\le m-3<1\iff 0\le m<4$ .

Câu 2.

a. Xét phương trình $x^2+{\left(\frac{x}{x+1}\right)}^2=3$

Điều kiện xác định $x+1\ne 0\iff x\ne -1$ .

Ta có:

$\begin{array}{cc}& x^2+{\left(\frac{x}{x+1}\right)}^2=3\\ & \iff {\left(x-\frac{x}{x+1}\right)}^2+2x.\frac{x}{x+1}=3\\ & \iff {\left(\frac{x^2}{x+1}\right)}^2+2.\frac{x^2}{x+1}-3=0\end{array}$ .

Đặt $t=\frac{x^2}{x+1}$ , phương trình trở thành: $t^2+2t-3=0$

$\iff [\begin{array}{c}t=1\\ t=-3\end{array}$

+) $\frac{x^2}{x+1}=1\iff x^2-x-1=0$

$\iff x=\frac{1\pm \sqrt{5}}{2}$   (thỏa mãn điều kiện).

+) $\frac{x^2}{x+1}=-3\iff x^2+3x+3=0$  Vô nghiệm.

Vậy phương trình có hai nghiệm $x=\frac{1\pm \sqrt{5}}{2}$

b.Xét phương trình $\frac{x+m-1}{x+1}+\frac{x-2}{x}=2$   (1).

Điều kiện xác định $\{\begin{array}{c}x\ne -1\\ x\ne 0\end{array}$ .

Với điều kiện trên thì phương trình tương đương

$x^2+\left(m-1\right)x+x^2-x-2=2x^2+2x$

$\iff \left(m-4\right)x=2$      (2).

Phương trình (1) vô nghiệm khi và chỉ khi phương trình (2) vô nghiêm hoặc có nghiệm không thỏa mãn điều kiện.

+ Phương trình (2) vô nghiệm khi và chỉ khi $m-4=0\iff m=4$ .

+ Phương trình (2) có nghiệm khi và chỉ khi $m-4\ne \iff m\ne 4$ .

Khi đó nghiệm của (2) là $x=\frac{2}{m-4}$ .  Hiển nhiên $\frac{2}{m-4}\ne 0$

Nghiệm này không thỏa mãn điều kiện khi và chỉ khi

$\frac{2}{m-4}=-1$

$\iff 2=-m+4\iff m=2$

Vậy phương trình (1) vô nghiệm khi và chỉ khi m= 4 hoặc m= 2.

Câu 3.

Xét hệ $\{\begin{array}{c}{x}_1+x_2+x_1{x}_2=0\\ \left(m-1\right)\left(x_1+x_2\right)-x_1{x}_2=3m-1\end{array}$

Đặt $S=x_1+x_2,P=x_1{x}_2$ .

Hệ trở thành $\{\begin{array}{c}S+P=0\\ \left(m-1\right)S-P=3m-1\end{array}$

$\iff \{\begin{array}{c}mS=3m-1\\ P=-S\end{array}$

Để hệ có nghiệm thì $m\ne 0$ . Khi đó: 

$\{\begin{array}{c}S=\frac{3m-1}{m}\\ P=-\frac{3m-1}{m}\end{array}$

Vậy phương trình bậc hai cần tìm là

$\begin{array}{cc}& x^2-\frac{3m-1}{m}x-\frac{3m-1}{m}=0\\ & \iff m{x}^2-\left(3m-1\right)x-3m+1=0\end{array}$ .

Câu 4.

Xét phương trình $2x+\sqrt{x-1}=m-1$    (1)

Điều kiện xác định: $x-1\ge 0\iff x\ge 1$ .

Đặt $t=\sqrt{x-1},t\ge 0$ . Phương trình trở thành

$2\left(t^2+1\right)+t=m-1$

$\iff 2t^2+t+3-m=0$   (2).

Phương trịnh (1) có nghiệm khi và chỉ khi phương trình (2) có nghiệm $t\ge 0$ .

Có hai trường hợp

+ Phương trình (2) có hai nghiệm thỏa mãn điều kiện $t_1\le 0\le t_2$

$P⩽0\iff \frac{3-m}{2}⩽0\iff m⩾3$

+ Phương trình (2) có hai nghiệm thỏa mãn điều kiện $0\le t_1\le t_2$

$\{\begin{array}{c}\Delta \ge 0\\ S\ge 0\\ P\ge 0\end{array}\iff \{\begin{array}{c}1-8\left(3-m\right)\ge 0\\ -\frac{1}{2}\ge 0\\ \frac{3-m}{2}\ge \end{array}$ . Không có m thỏa mãn các điều kiện này.

Vậy phương trình (1) có nghiệm khi $m\ge 3$ .