Đề bài
Câu 1. Cho tam giác ABC vuông tại A có trọng tâm là G. Biết rằng AB=6 và AC=8. Tính độ dài của các véc tơ −−→GB−−−→GC và −−→GB+−−→GC.
Câu 2. Cho hai hình bình hành ABCD và AMNP có chung đỉnh A. Chứng minh rằng −−→BM+−−→DP=−−→CN.
Câu 3. Cho hình bình hành ABDC tâm O. Gọi G là trọng tâm tam giác OCD. Hãy biểu thị −−→BG theo các véc tơ −−→AB và −−→AC.
Lời giải chi tiết
Câu 1.
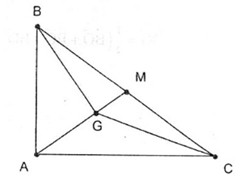
Theo định lí Pitago ta có: BC=√AB2+AC2=√36+64=10
Ta có −−→GB−−−→GC=−−→CB . Suy ra ∣∣∣−−→GB−−−→GC∣∣∣=∣∣∣−−→CB∣∣∣=CB=10
Gọi M là trung điểm BC. Ta có −−→GB+−−→GC=2−−→GM .
Mà GM=13AM=16BC=106=53
Vậy ∣∣∣−−→GB+−−→GC∣∣∣=∣∣∣2−−→GM∣∣∣=2GM=103
Câu 2.
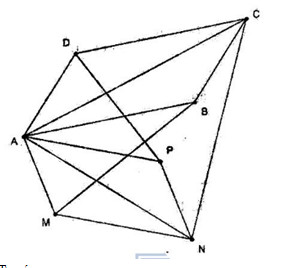
Ta có
−−→BM+−−→DP
=−−→AM−−−→AB+−−→AP−−−→AD
=(−−→AM+−−→AP)−(−−→AB+−−→AD)
=−−→AN−−−→AC=−−→CN
Câu 3.
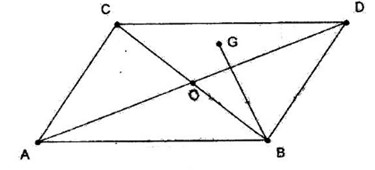
Ta có:
−−→BG=13(−−→BO+−−→BC+−−→BD)
=13(12−−→BC+−−→BC+−−→AC)=13(32−−→BC+−−→AC)=12−−→BC+13−−→AC=12(−−→AC−−−→AB)+13−−→AC=12−−→AC−12−−→AB+13−−→AC=−12−−→AB+56−−→AC




0 Nhận xét